Něco málo o číselných soustavách

Číselné soustavy, se kterými přijdete při programování 8051 do styku: desítková, dvojková, šestnáctková
Nejvíce bude potřeba seznámit se s binární (dvojkovou) a hexadecimální (šestnáctkovou) soustavou

Binární soustava (dvojková)
Základ soustavy je 2. Může nabývat hodnoty 0 nebo 1. Začneme s 8-bitovým číslem, se kterým se u 8051 setkáte nejčastěji. 8-bitovým binárním číslem lze tedy zapsat celé číslo od 0 do 255, což odpovídá hodnotě 28. To platí v případě, že zapisovaná čísla uvažujeme bez znaménka. Pokud bychom chtěli zapisovat kladná i záporná čísla (se znaménkem), pro znaménko se vyhradí nejvyšší bit(nejvíce vlevo).Z toho vyplývá, že pro zapsání samotného čísla nám zůstane 7 bitů, což odpovídá zobrazitelnému rozsahu 128. Připočteme-li ještě nulu (počítá jako součást kladných čísel), můžeme zapsat čísla s uvažováním znaménka v rozsahu od -128 do +127. Uvedeme si několik příkladů zápisu takových čísel:
8-bitová čísla bez znaménka 8-bitová se znaménkem
dekadicky - binárně dekadicky - binárně
0 - 00000000 -128 - 10000000
1 - 00000001 -106 - 10010110
9 - 00001001 -88 - 10101000
88 - 01011000 -9 - 11110111
106 - 01101010 -2 - 11111110
255 - 11111111 -1 - 11111111
0 - 00000000
+1 - 00000001
+2 - 00000010
+9 - 00001001
+88 - 01011000
+106 - 01101010
+127 - 01111111
Pokud chceme převést kladné číslo na záporné (téže hodnoty), musíme kladné číslo převést na tzv. doplňkový kód (dvojkový doplněk). To se provede tak, že v binárním vyjádření kladného čísla provedeme negaci a následně k nejnižšímu řádu (pozice nejvíce vpravo) přičteme 1 dle pravidel pro sčítání ve dvojkové soustavě.

Existují i jiné způsoby vyjádření záporných čísel než je dvojkovým doplňkem. Nejjednodušší je způsob, kdy se ke dvojkově vyjádřenému číslu předřadí jedno místo (bit), které má význam znaménka odděleně od hodnoty čísla. V případě 8-bitového registru pak bude v nejvyšším=8.bitu zapsáno znaménko (0 = +, 1 = -), ve zbylých 7 bitech pak bude samotné číslo zapsané absolutně, tj.jakoby kladné. Tomuto způsobu vyjádření se říká přímý kód.
Dalším způsobem vyjádření záporného čísla je logický doplněk. Ten se vytvoří tak, že se provede inverze (=negace) dvojkově zapsaného čísla, tj.zamění se nuly za jedničky a opačně. U tohoto způsobu lze nulu v případě n-bitového čísla zapsat buď jako n nul nebo jako n jedniček. Nejvhodnější způsob vyjádření záporného čísla ale zůstává dvojkový doplněk, se kterým budeme dále uvažovat.

Pokud budeme v programu pro 8051 potřebovat převést nějaké číslo na dvojkový doplněk, uděláme to jednoduše použitím instrukce CPL a ADD. Příklad pro převod čísla ve střadači: 
CPL A
ADD A,#1
Základní operace ve dvojkové soustavě
Sčítání Odčítání Násobení
0+0=0 0-0=0 0.0=0
0+1=1 0-1=0 a přenos 1 do nižšího řádu 0.1=0
1+0=1 1-0=1 1.0=0
1+1=0 a přenos 1 do vyššího řádu 1-1=0 1.1=1


Sčítání a odčítání 8-bitových čísel bez znaménka
- provede se sečtení dle pravidel pro sčítání a odčítání ve dvojkové soustavě. Operaci odčítání je možné převést na operaci sčítání s tím, že menšitele převedeme na dvojkový doplněk a pak teprve přičteme k menšenci.

Sčítání a odčítání 8-bitových čísel se znaménkem
- provede se sečtení dle pravidel pro sčítání a odčítání ve dvojkové soustavě, operaci odčítání je možné převést na operaci sčítání s tím, že menšitele převedeme na dvojkový doplněk a pak teprve přičteme k menšenci. Rozsah zobrazitelných čísel (kladných i záporných) si lze představit jako uzavřenou kružnici, ve které kladná čísla "přetíkají" do záporných a naopak.

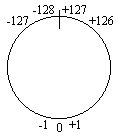
Kružnice znázorňující přetékání čísel

Uvedeme si několik příkladů pro čísla se znaménkem:
+127 0111 1111 -128 1000 0000
+1 0000 0001 -1 1111 1111
-128 1000 0000 +127 10111 1111
Jak jste si asi všimli, u druhého příkladu vznikl ve výsledku přenos (1 v nejvyšším, nyní 9.bitu). O takovémto přenosu se jěště dále zmíníme.

A takto bude vypadat sčítání 8-bitových čísel v assembleru 8051:
Provede se sečtení pomocí instrukce ADD s tím, že do bitu C se zapíše případný přenos (přesněji - vznikl-li přenos, pak v C bude 1; nevznikl-li přenos - v C bude 0).
Dále může dojít k nastavení bitu OV. Stav bitu OV po sčítání má význam při sčítání čísel se znaménky, při sčítání čísel bez znamének nás nemusí zajímat.
Bude lepší, když si teď připomeneme význam bitů C a OV.

C - Přenos (Carry) je nastaven při aritmetické operaci, při které dochází k přenosu z osmého do devátého bitu a při některých instrukcích porovnání.

OV - Příznak přetečení (Overflow) indikuje přetečení při aritmetické operaci sčítání nebo odčítání, jestliže zpracovávaná čísla považujeme za čísla se znaménkem. Jedná se o případ, kdy součet dvou záporných čísel je kladný (došlo k přenosu mezi devátým a osmým bitem a nedošlo k přenosu mezi osmým a sedmým bitem) nebo součet dvou kladných čísel je záporný (nedošlo k přenosu mezi devátým a osmým bitem a došlo k přenosu mezi osmým a sedmým bitem), kde osmý bit představuje znaménko. Příznak je též využíván při operaci dělení k identifikaci dělení nulou a při instrukci násobení.

Bit OV se tedy nastaví např. při sčítání čísel +127 a +1, kde výsledek je -128, nebo při sčítání čísel -128 a -1, kde výsledek je +127, atd. Blíže bylo vysvětleno výše v odstavci o "kružnici přetíkání".

Následující jednoduchý příklad ukazuje sčítání dvou čísel (se znaménky i bez), 1.číslo je uloženo v R1, 2.číslo je uloženo v R2. Výsledek bude v Acc. Funkci si ověřte třeba v Miťáckém simulátoru. 
        org 0
        jmp start
        org 30h
start:  mov a,r2
        add a,r1
konec:  jmp konec
end
Sledujte stavy bitů C a OV po provedení programu pro různá sčítaná čísla. Např. po sečtení +127 a +1 se nastaví jen OV (výsledek je záporný), C se nuluje, protože nedošlo k přenosu.
Po sečtení -128 a -1 se nastaví OV (výsledek je kladný), C se nastaví na 1, protože došlo k přenosu do 9.bitu (výsledek jakoby věší než 255). A taky něco jiného: +106(6AH) a +88(58H), výsledek -67(C2H),OV=1,C=0.

Stavy C a OV se samozřejmě mění i při práci s čísly bez znaménka, tady nás zajímá ale pouze bit C, ten se nastaví, pokud je výsledek sčítání větší než 255. Bit C nám tedy může sloužit k identifikaci nesmyslného výsledku v Acc, právě pokud je výsledek větší než 255.

Při odčítání 8-bitových čísel pomocí instrukce SUBB je nutné pamatovat na to, že se kromě odčítaného čísla odčítá od obsahu Acc i bit C.

Sčítání a odčítání 16-bitových čísel
Provádí se jako sečtení vyššího a nižšího řádu čísla zvlášť s respektováním případného přenosu z nižšího řádu do vyššího. Jinými slovy nejprve sečteme nižší řády (8 a 8 bitů) obou čísel, potom sečteme vyšší řády (opět 8 a 8 bitů) sčítaných čísel s respektováním případného přenosu vzniklého po sečtení nižších řádů. A nakonec to dáme celé dohromady - výsledek tedy bude ve 2 registrech (16 bitů).

Ukážeme si příklad pro sečtení dvou 16-bitových čísel bez znaménka. 1.číslo je umístěno na adresách 30H,31H (vyšší řád,nižší řád), 2.číslo je umístěno na adresách 40H,41H (vř,nř). Výsledek bude uložen na adresy 50H,51H (vř,nř).

Sčítání
        org 0
        jmp start
        org 30h
start:  mov a,31h
        add a,41h
        mov 51h,a
        mov a,30h
        addc a,40h
        mov 50h,a
konec:  jmp konec
end
Odčítání
        org 0
        jmp start
        org 30h
start:	clr c
        mov a,31h
        subb a,41h
        mov 51h,a
        mov a,30h
        subb a,40h
        mov 50h,a
konec:  jmp konec
end
Při sčítání je tedy nutné nižší řády obou čísel mezi sebou sečíst instrukcí ADD, vyšší řády sečíst instrukcí ADDC. Při případném přenosu výsledku se nastaví bit C.
Při odčítání je nutné nejdříve nulovat bit C, aby nám jeho předchozí stav neovlivnil odčítání nižších řádů. Poté mezi sebou odečteme nižší řády obou čísel instrukcí SUBB, nyní nesmí dojít ke změně bitu C (aby byl zachován případný vzniklý přenos) a provedeme vzájemné odečtení vyšších řádů opět instrukcí SUBB.

Sčítání a odčítání 16-bitových čísel se znaménkem jsem dosud nepotřeboval, věřím, že je lépe se tomuto ve vlastním zájmu vyhnout.

Násobení 8-bitových čísel

Násobení se převádí na opakované sčítání. Násobence postupně sčítáme tolikrát , kolikrát to předepisuje hodnota příslušného řádového koeficientu násobitele. Jinými slovy jde o staré známé sepisování.

Příklad násobení:
10011001 . 1011  =>>  153 . 11 = 1683
------------------
10011001
 010011001
   10011001
-----------
11010010011(2)  =>> 1683(10)
Násobení 8-bitových čísel bez znaménka v assembleru 8051:
Pro operaci násobení mikroprocesor disponuje instrukcí MUL AB, která mezi sebou vynásobí dvě 8-bitová čísla, kde jedno je uloženo ve střadači a druhé v registru B. Nižší byte výsledku se uloží zpět do střadače, vyšší byte se uloží do registru B. Po provedení instrukce se vynuluje příznakový bit C a dále se nastaví příznakový bit OV, pokud má výsledek hodnotu větší než 255 (výsledek je tedy větší než 8-bitový). Pokud je výsledek menší než 255, příznak OV se vynuluje (výsledek max. 8-bitový).

Příklad:
Vynásobte dvě 8-bitová čísla bez znaménka, 1.číslo je v R1, 2.číslo v R2, výsledek uložte do R3,R4 (vř,nř).
        org 0
        jmp start
        org 30h
start:  mov b,r1
        mov a,r2
        mul ab
        mov r3,b
        mov r4,a
konec:	jmp konec
end


Násobení 8-bitových čísel se znaménkem

Už to začíná být trochu složitější. Je třeba si uvědomit, že nemůžeme násobit 2 čísla, pokud je jedno z nich uvažováno bez znaménka a druhé se znaménkem. Můžeme samozřejmě násobit 2 čísla, kdy jedno bude kladné a druhé záporné, ale obě musejí být vždy uvažována se znaménkem - tedy obě vyjádřena buď dvojkovým doplňkem nebo přímým kódem (tj. ve tvaru znaménko/absoluní hodnota). Největší násobenec i násobitel tedy může být číslo v rozsahu -128 až +127.
Pokud jsou násobená čísla vyjádřena v přímém kódu (tj. v 8.bitu znaménko a ve zbývajících 7 bitech číslice absolutně=bez znaménka), vynásobí se jejich absolutní hodnoty podle algoritmu pro kladná čísla a znaménkový bit se k výsledku doplní dodatečně. Pokud jsou násobená čísla vyjádřena dvojkovým doplňkem, musí se před operací násobení převést do přímého kódu.

Příklad:
Vynásobte dvě 8-bitová čísla se znaménkem, 1.číslo je v R1, 2.číslo v R2, výsledek uložte do R3,R4 (vř,nř).


Násobení 16-bitových čísel


Dělení 8-bitových čísel

Dělení se převádí na odečítání a posunutí o řád.

Příklad dělení:
11010001 : 1011  =>>  209 : 11 = 19


Pro práci se simulátorem, třeba právě s tím od firmy MITE, se vám určitě bude hodit převod dekadického čísla (se znaménkem i bez), příp. binárního do hexadecimálního tvaru a naopak.

Hexadecimální soustava (šestnáctková)
Základ soustavy je 16. Prvních deset vyjadřovaných číslic soustavy se zapisuje číslicemi 0 až 9, zbylých šest číslic se zapisuje jako prvních šest písmen abecedy, tedy A až F. U 8051 se stále pracuje s 8-bitovými čísly (registry po 8 bitech), při práci s nimi jde tedy jen různou formu zápisu těchto 8-bitových čísel. Někdy je potřebujeme vyjádřit dekadicky, jindy binárně a někdy právě hexadecimálně. S hexadecimálním zápisem se nejčastěji setkáte např. při ladění a zkoušení programu v simulátoru (třeba s tím od MITE), kde většina registrů vypisuje právě v hexadecimální soustavě z důvodu úspory místa na obrazovce. Zobrazení dekadicky není praktické (simulátor neví jestli jsou zobrazovaná čísla uvažována se znaménky nebo ne), výpis v binární soustavě zabere 8 pozic na obrazovce pro jediný registr. V hexadecimální soustavě je potřeba k zobrazení obsahu registru pouze 2 míst.
POZN: Pokud píšete program v assembleru 8051, je nutné při zápisu čísel v hexadecimální soustavě, které začínají písmeny A až F, připsat před takovéto číslo nulu.
Příklad: není možné zapsat MOV A,#FFH >>>> je nutné číslo zapsat takto: MOV A,#0FFH


Pro pohodlnou práci nejen se zmiňovaným simulátorem tedy bude nejdůležitější zvládnout převody z binární, příp. dekadické (desítkové) soustavy do hexadecimální a naopak.

Převod čísla z dekadické soustavy do hexadecimální

Převod čísla 0 až 16 (dek) zvládneme zpaměti - 0 až F (hex). Převod většího čísla provedeme postupným dělením dekadického čísla základem hex.soustavy, tj. číslem 16 a sepisováním zbytku po celočíselném dělení. Výsledek dostaneme zapsáním všech zbytků v obráceném pořadí.

Příklad pro číslo 154(10) :
154 
9 
0 		  :16
 10
 9		 Zbytky po dělení zapíšeme "odspodu" - to je 9,10 a dostáváme tedy, že 154(10) = 9A(16)

Převod čísla z hexadecimální soustavy do dekadické

Převod provedeme dosazením hodnot odpovídajících převáděnému číslu do obecného polynomu pro převod do dekadické soustavy.
Polynom pro převod do dekadické soustavy
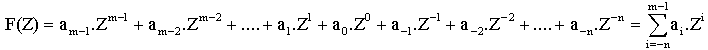
kde F(Z) je číslo vyjádřené v číselné soustavě o základu Z (v našem případě je Z=16)
ai jsou číselné koeficienty, kde i je <0,1,2....Z-1> (v našem případě koeficienty nabývají hodnot 0 až F)
m je počet řádových míst, na kterých má základ kladný exponent
n je počet řádových míst, na kterých má základ záporný exponent

n má význam tehdy, pokud převádíme desetinné číslo. My budeme v následujícím příkladě převádět číslo celé, takže nám část polynomu "odpadne"

Příklad pro číslo C3(16) :
C.161 + 3.160 = 12.16 + 3.1 = 195
C3(16) = 195(10)


Převod čísla z dekadické soustavy do binární

Převod čísla provedeme postupným dělením dekadického čísla základem binární soustavy, tj. číslem 2 a sepisováním zbytku po celočíselném dělení. Výsledek dostaneme zapsáním všech zbytků v obráceném pořadí.

Příklad pro číslo 215(10) :
215   :2
107   1 Zbytky po dělení zapíšeme "odspodu" - to je 11010111 a dostáváme tedy, že 215(10) = 11010111(2)
53   1
26   1
13   0
6   1
3   0
1   1
0   1


Převod čísla z binární soustavy do dekadické

Převod provedeme dosazením hodnot odpovídajících převáděnému číslu do obecného polynomu pro převod do dekadické soustavy (uveden výše u převodu z hexadecimální soustavy).
V následujících dvou příkladech si ukážeme převod jak celého, tak i desetinného čísla. Pro dosazení do polynomu tedy platí, že Z=2 a dále ai jsou číselné koeficienty, kde i je <0,1>.

Příklad pro celé číslo 10001010(2) :
1.27 + 0.26 + 0.25 + 0.24 + 1.23 + 0.22 + 1.21 + 0.20 = 128 + 8 + 2 = 138
10001010(2) = 138(10)

Příklad pro desetinné číslo 101101,101(2) :
1.25 + 0.24 + 1.23 + 1.22 + 0.21 + 1.20 + 1.2-1 + 0.2-2 + 1.2-3 = 32 + 8 + 4 + 1 + 1/2 + 1/8 = 45 5/8
101101,101(2) = 45 a 5/8(10)


S převody čísel z jedné soustavy do druhé nám pomůže i jednoduchá kalkulačka přítomná ve všech verzích op.systému Windows, zrovna tak s ní můžeme provádět aritmetické operace v dané soustavě (zvládá binární, hexadecimální a samozřejmě i dekadickou soustavu). Pokud budete potřebovat pracovat s čísly se znamínkem, budete se muset poohlédnout po něčem specializovanějším.


Pro realizaci aritmetických operací s 16-bitovými nebo i 32-bitovými čísly (bez i se znaménkem) existují již hotové a ověřené krátké prográmky (rutiny) v assembleru 8051, které toto udělají za Vás. Na začátku takovéto rutiny je obvykle uvedeno, kde v paměti mají být umístěny vstupní data a pak je zde uvedeno, kde se bude nacházet výsledek. Takovéto rutiny Vám ušetří mnoho času.

Minimálně ve stejném množství existují i rutiny pro převody čísel mezi soustavami nebo kódy. Určitě se Vám někdy bude hodit např. rutina pro převod binárního čísla na kód ASCII a naopak.

Některé rutiny můžete nalézt na adrese www.8052.com. Zvláště užitečný a kompletní je soubor rutin pro sčítání,odčítání,násobení a dělení 8,16 i 32-bitových čísel se znaménkem nebo bez od Dr.Marshalla. Pokud zde nenajdete tu rutinu, kterou potřebujete, budete muset hledat jinde na Internetu.


Dekadická korekce - co to je ?

Pokud pracujete s mikropočítačem, zjistíte, že pro něj je vlastní způsob práce ve dvojkové soustavě, ale Vám je nejpřirozenější práce v desítkové soustavě. Abyste nemuseli vstupní data do mikroprocesoru převádět do dvojkové soustavy a naopak výstupní dvojková data z mikroprocesoru převádět na desítková, vznikla a používá se tzv. dvojkově desítková soustava. Mikroprocesor pak navenek pracuje desítkově. Jednotlivé číslice desítkového čísla (dekády) jsou zobrazeny skupinou dvojkových číslic. Pro zobrazení desítkového čísla se tedy používá nějaký kód, nejčastěji BCD kód (Binary Coded Decimal), někdy také označovaný jako kód 8421. Desítková číslice je pomocí tohoto kódu reprezentována jako čtyřmístné dvojkové číslo, maximálně lze tedy vytvořit 16 kombinací. Nám jich ale stačí jen 10 pro zobrazení číslic 0 až 9, nevyužité kódové kombinace odpovídající šestnáctkovým číslicím A až F (10 až 15) jsou tzv. zakázané stavy. Ty z pohledu přenosu dat představují určitou informační nadbytečnost.

Kód BCD (8421)
Desítková
číslice		 BCD (8421)
0 0000
1 0001
2 0010
3 0011
4 0100
5 0101
6 0110
7 0111
8 1000
9 1001

S jednotlivými dekádami čísla v BCD kódu zacházíme jako s dvojkovým číslem. Pokud je při sčítání výsledkem některá zakázaná kombinace nebo vznikl přenos, pak se k dílčímu výsledku v této dekádě přičte číslo 6 - což je rozdíl mezi základem šestnáctkové a desítkové soustavy. Stejně tak při odčítání se od mezivýsledku odečte číslo 6, pokud nabyl některé ze zakázaných hodnot. Tím je zajištěno, že vztahy mezi dekádami odpovídají vztahům mezi desítkovými číslicemi téhož čísla, a že tedy kombinace v jednotlivých dekádách odpovídají právě číslicím 0 až 9. Toto je tedy dekadická korekce.

Příklad sčítání:

 154(10) ==>>   0001 0101 0100(2/10)
+271(10) ==>> + 0010 0111 0001(2/10)


 425(10) ==>>   0011 1100 0101
Prostřední čtveřice (dekáda) výsledku je již v oblasti zakázaných kombinací (odpovídající číslici C a v desítkové soustavě by jí měla odpovídat číslice 2). Správného výsledku dosáhneme, pokud přičteme dvojkově k zakázané kombinaci číslo 6 (0110). Konečný výsledek tedy bude:
  0011 1100 0101
+      0110 


  0100 0010 0101(2/10)
 


 ==>> 425(10)

Příklad odčítání:

 571(10) ==>>   0101 0111 0001(2/10)
-356(10) ==>> - 0011 0101 0110(2/10)


 215(10) ==>>   0010 0001 1011
V poslední dekádě výsledku vyšla zakázaná kombinace (odpovídající číslici B a v desítkové soustavě by jí měla odpovídat číslice 5). Pokud od ní dvojkově odečteme desítkové číslo 6 (0110), dostaneme potom správný výsledek.
Konečný výsledek tedy bude:
  0010 0001 1011
-           0110


  0010 0001 0101(2/10)
 


 ==>> 215(10)
A jak funguje dekadická korekce u 8051...

Mikroprocesor nám nabízí speciální instrukci DA A, kterou lze provést dekadickou korekci střadače. Dekadická korekce zde funguje přesně tak, jak jsme si ji popsali výše. Dekadickou korekci lze ale provést jen po sčítání, velmi jednoduše můžeme sčítat dvě dvoumístná čísla v BCD kódu. Po sečtení dvou čísel (ADD A,zdrojový byte) zůstane výsledek ve střadači s tím, že pokud došlo k přenosu mezi 4. a 5.bitem střadače, nastaví se příznakový bit AC. Pokud došlo i k přenosu z 8.bitu střadače, nastaví se samozřejmě i příznakový bit C. Potom aplikujeme instrukci DA A, ta si zjistí, jestli je hodnota na čtyřech nižších bitech větší než 9 nebo je nastaven příznak AC, a jestli ano, pak ke střadači přičte hodnotu 6 (hexadecimálně). Potom si stejně tak zjistí, zda-li je hodnota na čtyřech vyšších bitech větší než 9 nebo je nastaven příznak C, a jestli ano, pak ke střadači přičte hodnotu 60 (hexadecimálně) - tedy pouze k vyšším čtyřem bitům, nižší čtyři bity zůstavájí nezměněny. Tím je provedena dekadická korekce.

Příklad:
v R0 je číslo 26 v BCD kódu
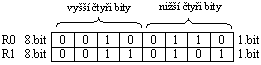v R1 je číslo 35 v BCD kódu		 Umístění BCD čísel v registrech R0 a R1 před sčítáním 


        org 0
        jmp start
        org 30H
start:  mov a,r0
        add a,r1
        da a
konec:  jmp konec
end
Pokud budete přůběh vykonávání programu sledovat v nějakém simulátoru, uvídíte, že po instrukci ADD bude ve střadači výsledek 5B a po instrukci DA tam už bude správný výsledek 61.


Zpět na hlavní stránku povídání

Copyright © Michal Fuksa 2001