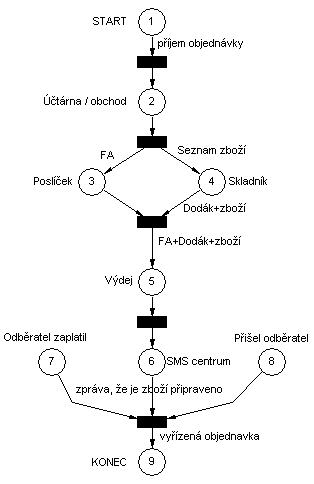
Petriho síť

 

Petriho sítě jsou jedním z nejpoužívanějších nástrojů pro modelování a návrh složitých systémů s paralelními procesy a hierarchickou strukturou. Mají nesčetné aplikace v oblasti zpracování dat, paralelního programování, operačních systémů, distribuovaných databází a řízení složitých procesů jakéhokoliv druhu včetně návrhu a modelování informačních systémů.

 

Petriho síť se opírá o bipartitní orientovaný graf N = (P; T;A), kde P je neprázdná množina

uzlů označovaných jako místa, T je neprázdná množina uzlů označovaných jako přechody a A

je množina orientovaných hran. Pro každou hranu a_i z množiny A platí a_i = (p_j ; t_k) nebo a_i = (t_j; p_k), hrana tedy spojuje buď místo p_j s přechodem t_k (místo p_j nazýváme vstupním místem přechodu t_k) nebo přechod t_j s místem p_k (místo p_k nazýváme výstupním místem přechodu tj ).

 

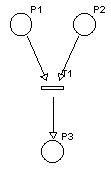Prvky sítě tedy jsou:                                                          Jednoduché schéma:

 

Místo Hrana Přechod          

 

Značená Petriho síť M = (P; T;A; m) vznikne doplněním grafu N o označení, každého místa p z množiny P přirozeným číslem m(p). Graficky se to vyjadřuje tečkou. Počet teček je shodný s číslem m(p).

Značenou Petriho síť lze použít například jako popis dynamického chování nedeterministických systémů podobně jako konečného automatu pro popis deterministických systémů.

 

Stav sítě je konkrétní značení dané Petriho sítě.

Dovolený (aktivní) přechod je přechod, který má všechny vstupy s m(p)>0, nebo-li ve všech místech vstupujících do přechodu je alespoň jedna tečka.

Změnami stav prochází Petriho síť svůj stavový prostor, což jsou všechny možné stavy Petriho sítě. Dosažitelné stavy jsou všechny stavy, do kterých se může Petriho síť dostat z počátečního stavu m₀ .

Síť považujeme za živou pokud lze z každého dosažitelného stavu přejít do jiného stavu. Pokud v dosažitelném stavu sítě nedojde k aktivaci alespoň jednoho přechodu, síť je zablokovaná (deadlock).

 

Stavový prostor Petriho sítì je obecně nekonečný. V praxi nás však zajímají zvláště sítě s konečným počtem stavů:

• bezpečná síť – v každém jejím stavu existuje v každém místě maximálně jedna tečka
• k-omezená síť – v každém jejím stavu existuje v každém místě maximálně k teček
• omezená síť – je-li to k-omezená síť a k je konečné
• konzervativní síť – v každém jejím stavu je v síti stejný počet teček

 

Graf dosažitelnosti je vlastně znázorněný automat, se shodným chováním jako daná Petriho síť. Tento graf může být značně rozsáhlý. Pro k-omezenou síť má (2^cardP)^k uzlů. Uzel grafu je stav Petriho sítě a hrana je dovolený přechod mezi stavy sítě.

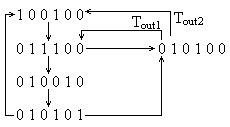
Příklad 1. Petriho síť simulující komunikaci mezi terminálem a SQL serverem, kde se při komunikaci může ztratit příslušný paket. Počáteční stav sítě je 100100, nebo-li do místa 1 a 4 dáme po jedné tečce.

 

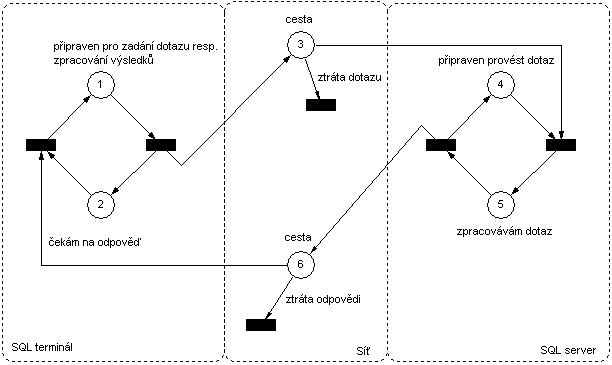
Tato síť má jeden hlavní nedostatek. V případě ztráty paketu s dotazem či odpovědí dojde k deadlocku. Proto síť doplníme o čas T_out1, po kterém dojde znovu k poslání dotazu a o čas T_out2, po kterém dojde ke zrušení operace a nastavení systému na zadání dalšího dotazu. T_out2> T_out1, aby to vůbec mělo nějaký smysl.

 

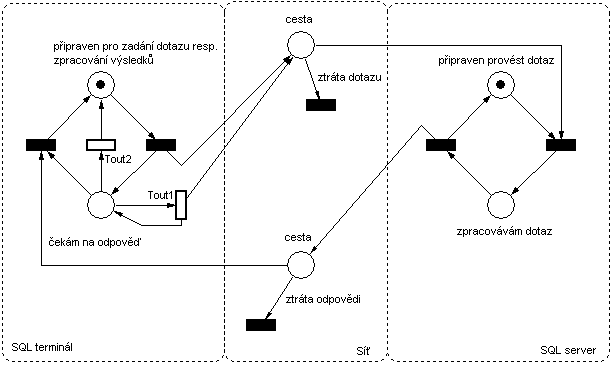
Graf dosažitelnosti:

 

 

Příklad 2. Petriho síť jako stavový diagram: