Vypracoval: Jiří Meixner,
sk.:Čt 12:45
Semestrální práce z předmětu Matematika 6f
Zadání:
Za 1. čtvrtletí 2001 se měnový kurz dolaru vůči koruně pohyboval dle tabulky. Spočtěte výběrový průměr XN, odhad střední hodnoty E(XN), výběrový rozptyl S2, výběrovou směrodatnou odchylku S, odhad rozptylu s2. Určete interval hodnot kurzu, v kterém by se mohl kurz dolaru pohybovat 1. týden 2.čtvrtletí s pravděpodobností P=0,95. Předpokládejte normální rozdělení a pro odhady použijte koeficient spolehlivosti 1-a = 0,95.
|
Týden |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
Kurz |
36,97 |
37,24 |
37,56 |
37,42 |
37,87 |
37,13 |
37,19 |
37,94 |
37,8 |
37,62 |
37,53 |
38,3 |
38,14 |
|
Pro n=12: |
t1-a |
t1-a/2 |
c21-a |
c21-a/2 |
c2a |
c2a/2 |
|
1-a=0,95 |
1,7823 |
2,1788 |
21,026 |
23,337 |
5,226 |
4,4038 |
Řešení:
Maximum=38,3
Minimum=36,97
Výběrový průměr XN :
![]()
Výběrový rozptyl S2:
![]()
Výběrová směrodatná odchylku S:
![]()
Odhad střední hodnoty E(XN):
![]()
![]()
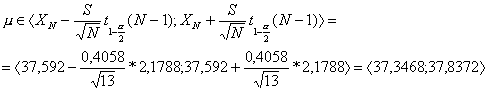
Odhad rozptylu s2:
![]()
![]()
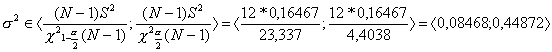
Interval hodnot kurzu s pravděpodobností P=0,95:
Čebyševova nerovnost:
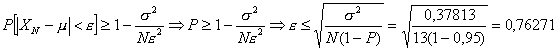
Interval kolem maximálního m=37,7926 tedy je: <37,4112;38,174>
Centrální limitní věta:
![]()
![]()
Interval kolem maximálního m=37,7926 tedy je: <37,6306;37,9546>