Domácí úloha číslo 1. : Problém batohu

1) Zadání : Naprogramujte řešení 0/1 problému batohu a) hrubou silou, b) heuristikou podle poměru cena/váha.

2) Vypracování : Pro řešení zadaného problému jsem jako vhodný programovací jazyk zvolil Borland C++ Builder 5. Zdrojový program i spustitelný soubor jsou přiloženy.

3) Rozbor řešení :

Hrubá síla : Metoda hrubé síly spočívá v prozkoušení všech možných kombinací a hledání optimálního řešení projitím celého stavového prostoru. Všech možností je 2^(počet věcí v batohu).  Takže se nabízí procházet postupně kombinace věcí v batohu od čísla 0 do 2^(počet věcí v batohu), kde binární zobrazení čísla by reprezentovalo obsah batohu (0/1 znamená nepatří/patří věc do batohu). Pořadí věcí by odpovídalo pořadí ze vstupního souboru. Jelikož daný jazyk má nanejvýš 64 bitový integer byli bychom omezeni na maximální počet 64 věcí v batohu. Proto si stav, zda-li věc patří či nepatří do batohu bude udržovat sama věc. Postup, ale zůstane zachován. Postupně se budou procházet stavy dle následující metodiky. Vždy se začne od první věci, pokud věc do batohu patří, tak se z něho vyndá a přejde se na další věc, pokud ale do batohu věc nepaří, tak se do něho přidá a tím nám vznikne nový stav batohu, pro který spočteme cenu a váhu, přičemž jakmile v mezisoučtu obdržíme větší váhu než je kapacita batohu , tak přejdeme na další stav, aniž bychom tento dopočítávali. Poslední stav je ten, ve kterém patří do batohu všechny věci a tím celý výpočet ukončíme. V průběhu výpočtu si samozřejmě musíme pamatovat nejlepší stav i s jeho cenou a vahou, který nám na konci výpočtu značí optimální řešení. Za lepší stav při stejné ceně se považuje ten lehčí.

Heuristika : Jako heuristickou metodu jsem použil seřazení pole věcí algoritmem Quick-sort dle ceny, váhy a poměru cena/váha. Ze seřazeného pole jsem pak přidával do batohu věci, které se tam co do váhy vešly a zároveň počítal celkovou cenu věcí v batohu.

4) Naměřené hodnoty :

Hrubá síla : Testování této metody bylo praktikováno pouze pro počty věcí v batohu do 25. Nad tento počet již byla časová náročnost algoritmu neúnosná, jak je vidět z tabulky.

 

 

Je vidět, že s každým dalším prvkem stoupala časová složitost přibližně dvojnásobně. To se dalo celkem předpokládat, jelikož s každým přidaným prvkem se zdvojnásobuje i stavový prostor. Samozřejmě, že navíc musíme počítat se zvyšujícím se režijním časem pro počítání ceny, porovnání s dosavadním maximem, popřípadě jeho výměnou apod.

 

Heuristika : Při použití heuristiky byly časy do zkušebních 40 věcí menší než přesnost použité metody měření času, která je setina sekundy.

Při použití heuristiky nebylo nalezeno vždy nejlepší řešení jako metodou hrubé síly. Průměrná procentuální chyba a průměrná procentuální chyba na celý soubor 50-ti instancí oproti optimálnímu řešení uvádí následující grafy.

 

 

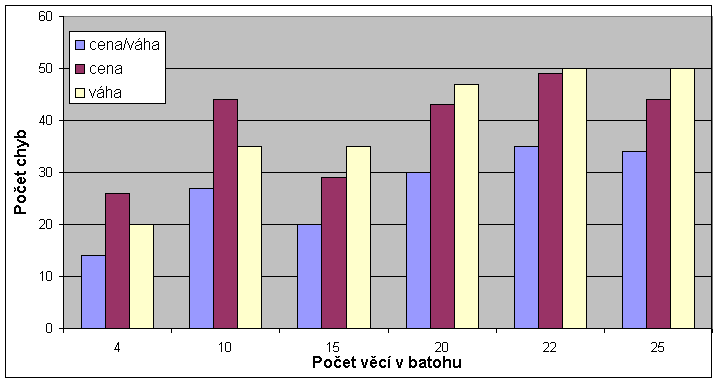
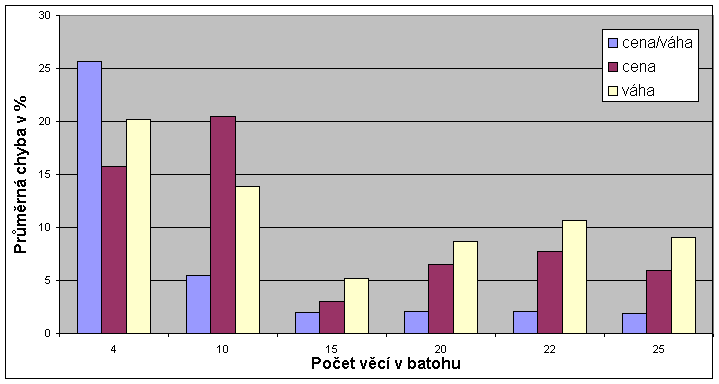
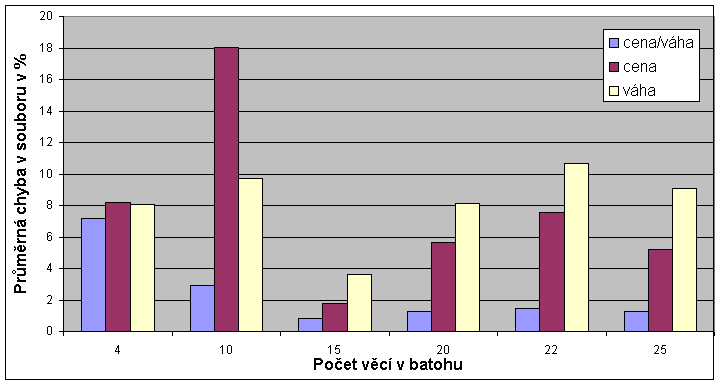
5) Závěr :

Z naměřených výsledků je jasně patrné, že heuristika dle poměru cena/váha se celkem dostatečně blíží optimálním výsledkům především při větším počtu věcí v batohu, za mnoho řádově menší čas potřebný k výpočtu než potřebuje metoda hrubé síly. Pokud, ale jsou třeba 100% nejlepší výsledky, je nutné si na ně nějakou dobu počkat.

Soubor cpp
Spustitelny soubor EXE