Vypracoval: Jiří Meixner

Úloha 5:

Problém obchodního cestujícího

Zadání:

Problém obchodního cestujícího je specifikován následovně. Musí se navštívit každé z N měst a to právě jednou nebo modifikované řešení, alespoň jednou. Na konci své cesty se musí vrátit zpět do počátečního města. Úkolem je najít minimální cestu, nebo-li pořadí jednotlivých měst tak, aby projitá vzdálenost byla minimální.

Zadání instancí problému je dáno distanční maticí, neboli tabulkou udávající vzdálenosti mezi danými dvěma městy.

Problém obchodního cestujícího patří mezi jedny z nejvíce studovaných problémů v kombinatorické optimalizaci. Problém jako takový je jednoduše formulovatelný, ale těžko řešitelný.

 

Rozbor řešení:

Problém obchodního cestujícího patří do množiny NP-úplných problémů. To je třída problémů, pro něž se zatím nepovedlo najít polynomiální algoritmus a jejichž časová složitost je pravděpodobně exponenciální. Pokud by však byl nalezen polynomiální algoritmus pro jeden z NP-úplných problémů je jisté že existují polynomiální algoritmy i pro všechny ostatní. Obecně se však věří, že pro tuto třídu žádný polynomiální algoritmus neexistuje.

Není však vyloučeno, že existuje algoritmus, jehož průměrná doba výpočtu je polynomiální. Problém obchodního cestujícího však můžeme vyřešit za pomocí heuristických algoritmů, které nedávají vždy optimální řešení, ale snaží se k němu přiblížit, což se jim daří s chybou až v řádu jednotek procent.

Pro řešení TSP lze například použít algoritmus založený jen na přidávání nejbližšího souseda k danému městu což je konstruktivní řešení. Tento algoritmu je však velmi jednoduchý a proto nedosahuje nejlepších výsledků. Vzdálenosti na počátku cesty budou krátké, ale se zmenšujícím se počtem měst se budou velmi prodlužovat. Tento algoritmus je však vhodný pro použití k nalezení počáteční cesty a následné optimalizace.

K optimalizaci či-li zlepšování cesty můžeme například použít algoritmus zvaný 2-opt pak se jedná o iterativní řešení. Algoritmus je založen na nahrazování dvou hran grafu (města jsou uzly a silnice jsou hrany) v cestě jinými dvěmi hranami tak, aby se celková délka cesty zlepšila. Pokud již žádnou záměnou nelze řešení zlepšit je cesta 2-optimální. Podobně lze použít i algoritmu 3-opt, obecně pak n-opt. Platí ovšem, že řešení za použití 3-opt je mnohem lepší než 2-opt, ale 4-opt se již vzhledem k poměru své složitosti ku zlepšení oproti 3-opt nevyplatí implementovat. Úplným zobecněním tohoto principu vznikl Linův-Kernighanův algoritmus zvaný  k-opt, kde k se v průběhu výpočtu mění. Jedná se o vysoce efektivní algoritmus. Mezi další algoritmy pak patří například tabu prohledávání, simulované ochlazování a jeho modifikace, genetické algoritmy a elastické neuronové sítě (pouze pro euklidovské TSP). Mnoho z těchto algoritmů má analogii v přírodě, jelikož z přírody jsou známy podobné problémy.

 

Popis použitých algoritmů:

Řešení lze nalézt dle následujících kroků:

1. Nalezení počáteční cesty (nějaká cesta)
1. Výběr počátečního města
2. Prodlužování cesty dokud v ní nejsou všechny města
3. Modifikace cesty tak, aby se poslední město dalo spojit s prvním
2. Optimalizace počáteční cesty (hledání minimální cesty)

 

Algoritmus pro nalezení počáteční cesty je de facto algoritmus pro nalezení Hamiltonovy kružnice. Implementovaný algoritmus funguje dle následujících bodů:

1. Vyberte počáteční město s nejvíce silnicemi, aby se zvýšila pravděpodobnost spojení posledního města s počátečním.
2. Prodlužujte cestu o další město, neexistující v cestě, dokud to jde. Vyzkoušel jsem následující prodlužování (existují i další):
1. O první město spojené s posledním.
2. O město s minimálním počtem silnic spojené s posledním.
3. O město s maximálním počtem silnic spojené s posledním.
4. O město s nejkratší silnicí s posledním městem.
3. Pokud jsou v cestě obsažena všechna města a poslední město lze spojit s počátečním, tak je nalezena Hamiltonova kružnice. Konec algoritmu.
4. Modifikujte cestu:
1. Najděte nezakázanou silnici z města M v cestě vedoucí do posledního města P.
2. Silnici z města M do následujícího města N v cestě přidejte do zakázaných silnic.
3. Otočte pořadí měst (orientaci silnic) v cestě od města N do konce, nebo-li N se stane posledním městem a P se stane následníkem M.
5. Pokud došlo k modifikaci cesty, tak jděte zpět na bod 2.
6. Vložte do cesty město neexistující v cestě, nebo-li hledejte město neexistující v cestě, které má silnici s městem v cestě i s jeho následovníkem. Takto zkoušejte všechna města neexistující v cestě.
7. Pokud jsou v cestě obsažena všechna města a poslední město nelze spojit s počátečním:
1. Vkládejte poslední město do cesty dokud to jde nebo dokud ho nelze spojit s počátečním.
2. Pokud lze spojit poslední město s počátečním, tak je nalezena Hamiltonova kružnice. Konec algoritmu.
3. Vložte první město do cesty.
4. Pokud lze spojit poslední město s počátečním, tak je nalezena Hamiltonova kružnice. Konec algoritmu.
5. Pokud došlo k modifikaci cesty v bodě 7c, tak jděte zpět na bod 7.
8. Pokud došlo k modifikaci cesty v bodě 6, tak jděte zpět na bod 6.
9. Vytvořte pěšinku:
1. Na městech, neexistujících v cestě, nalezněte cestu2 dle tohoto algoritmu (nemusí dojít ke spojen posledního města s prvním).
2. Pokud je cesta2 neprázdná, tak ji spojte s cestou fiktivní silnicí, kterou nazvěte pěšinka a ohodnoťte ji nekonečnem (velké číslo).
3. Pokud je cesta2 prázdná, tak spojte pěšinkou poslední město v cestě s počátečním a tím je nalezena Hamiltonova kružnice. Konec algoritmu.
4. Opakujte bod 9.

 

Pro optimalizaci počáteční cesty jsem zvolil simulované ochlazování:

1. Najdi dva páry silnic k prohození mezi sebou a zvyš čítač.
1. První město první silnice je následující město prvního z minulého volání
2. První město druhé silnice je voleno náhodně
2. Pokud by se po prohození párů cesta zlepšila tak je prohoď.
3. Pokud by se po prohození párů cesta zhoršila, ale zhoršení je v rámci okolí tak je také prohoď.(je splněna podmínka rand<exp(zlepseni/t) , kde zlepšení má vždy zápornou hodnotu.)
4. Pokud se čítač nedočítal na nastavenou horní mez, tak jdi zpět na bod 1.
5. Zmenši okolí dle funkce chladnutí. (okolí násobeno koeficientem chladnutí z (0-1) )
6. Pokud je okolí větší než minimální nastavené okolí, tak jdi zpět na bod 1.

 

Naměřené hodnoty:

Statistika měřených souboru:

 

Kvalita řešení ze simulovaného ochlazování je velmi závislá na vhodně zvolených parametrech a také na počátečním řešení, které optimalizuje. Existují zde následující parametry:

• T0  - počáteční teplota pro ochlazování
• Ch – koeficient chladnutí, pro funkci chladnutí z intervalu (0,1)
• ABS0 – absolutní nula, jako minimální teplota
• MAXITER – maximální počet iterací, horní mez čítače
• RAND – číslo z intervalu (0,1) pro podmínku při zhoršení cesty, je-li zadána 0 pak bude pokaždé jiné a to náhodné z <0,1>

 

Následující grafy znázorňují výsledky řešení pro soubory D a Testík při změně vždy jednoho z parametrů.

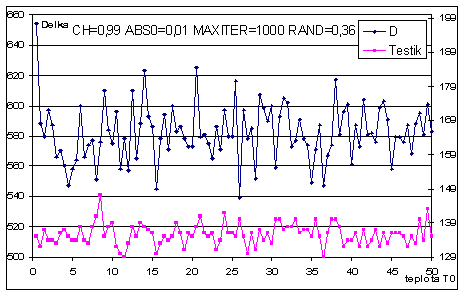
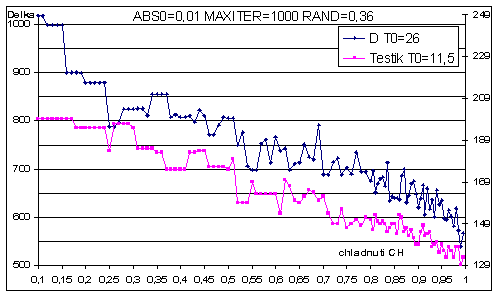
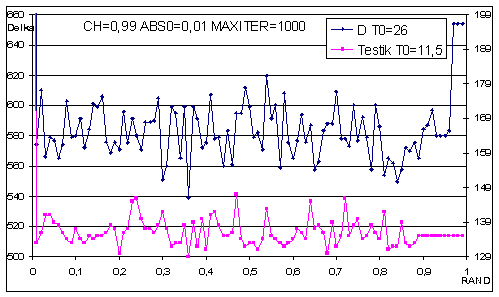
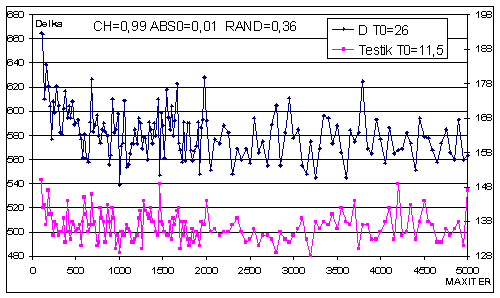
Dle těchto grafů jsem zvolil několik vhodných sad parametrů pro výpočet zadaných souborů. Pro velké soubory jsem při volbě parametrů ještě přihlížel na celkovou časovou náročnost výpočtu. Výsledky ukazuje následující tabulka.

 

Silně jsou vyznačeny nalezené minimální cesty. Čas výpočtu je pro ne kurzívou psané výsledky.

Průběh ochlazování pro soubory D, E a Testík při parametrech T0=5 resp. 26 Ch=0,99 ABS0=0,1 resp. 0,01 MAXITER=1000 a RAND=0,36 ukazuje následující graf.

 

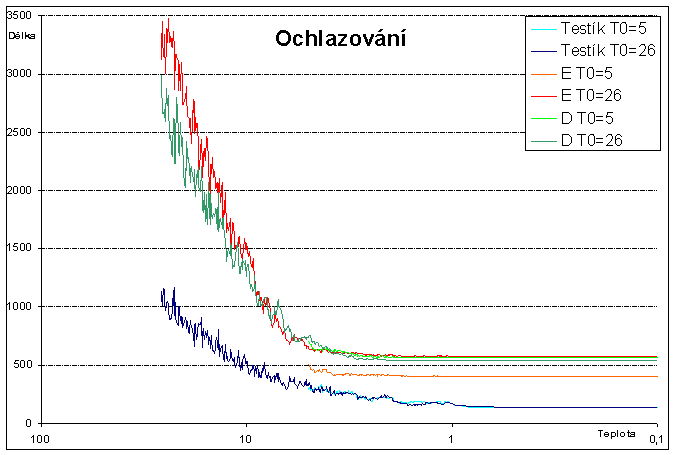
Závěr:

Jak již bylo řečeno simulované ochlazování je velice náchylné na vhodnou volbu parametrů a taktéž na počáteční řešení. Počáteční řešení jsem měnil dle strategie prodlužování (viz. bod 2 v algoritmu Hamiltonovské kružnice). Při volbě města s minimem nebo maximem silnic se vytvořilo vždy několik pěšin, které se však při ochlazování odstranily. Nejlepších výsledků jsem však dosáhl při strategii „nejbližší město“ a pro ni jsou také veškeré zde uváděné výsledky.

            Výsledky jsou taktéž závislé na funkci pro hledání párů hran k prohození. Opět jsem vyzkoušel několik strategií v závislosti na volbě prvních měst první a druhé silnice. Buďto jsem je volil náhodně nebo jako následníky resp. předchůdce prvního města první silnice resp. druhé silnice z minulého volání této funkce. Nejlepších výsledků jsem docílil při volbě prvního města první silnice jakožto následníka a náhodně zvoleného prvního města druhé silnice.

            Parametry ochlazování jsem zvolil dle grafů se změnami parametrů. I přesto je však nelze považovat za nejlepší, jelikož jsou mezi jednotlivými parametry ovlivňující vazby a já jsem vždy měnil pouze jeden z parametrů a ostatní zůstávali konstantní. Také platí, že nejvhodnější nalezené parametry jsou pouze pro daný soubor a pro jiný již neplatí. Z tohoto důvodu jsem si udělal statistiku daných souborů (viz. tabulka výše). Za velice překvapující považuji, že výsledek souboru E, který je dle statistiky velmi podobný souboru D, jsou  při použití „optimálních“ parametrů pro D tak špatný. Zřejmě u těchto souborů zprůměrování vytvořilo mylnou představu o podobnosti souborů. Na konec bych se chtěl ještě pozastavit u parametru RAND, jehož optimum vyšlo 0,36. exp(-1) je přibližně roven 0,36 což tedy znamená, že algoritmus ochlazování prohazuje hrany vždy, když dochází ke zlepšení a v případě zhoršení prohodí hrany pouze pokud je zhoršení menší než aktuální okolí reprezentované teplotou. Nebo-li čím menší je teplota tím méně může docházet ke zhoršování cesty.

 

Soubory ke stažení:

tsp.cpp – zdrojový soubor C++ programu vytvořený v Builderu 5

tsp.exe – spustitelný program,

bez parametrů, pak se dosadí T0=5, Ch=0.99, ABS0=0.01, MAXITER=1000, RAND=0.36

s parametry oddělenými mezerou v pořadí T0 Ch ABS0 MAXITER RAND

výstupy – adresář s výstupy jednotlivých souborů