Úvod

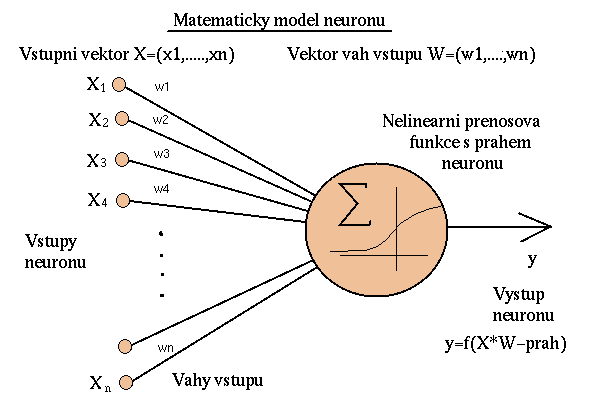
Abych Vás zavedl trochu do problematiky neuronových sítí, začneme zjednodušením. Neuron je elementární jednotka pro zpracování informace, podobně jako hradlo v integrovaných obvodech (tento text je určen mentálně narušeným posluchačům ČVUT FEL). Neuronová síť jsou propojené neurony (podle nějakého schématu, podobné např. Xilinxům pokud to snese srovnání). Neuronovou síť vymyslela matka příroda. Je to sice děvka, ale programovat umí dobře a efektivně. Neuronové sítě se osvědčily v těch nejsložitějších biologických systémech určených k přežití v jejich řízení. Neuronové sítě jsou obecně vzato černé krabice, do kterých se pouští data a na výstupu/ech vycházejí data zpracovaná, nějak závislá na datech vstupních. Neuronovou síť si lze představit jako asynchronní nestavový či stavový (vnitřní zpětné vazby) automat s tím, že data probíhající skrzevá dráty (v provedení matky přírody nervy) jsou analogová.

Jak to zaonačila matka příroda (to není pro elektrikáře až zase tak nezajímavé)

Příroda majíc k dispozici elektrochemické vodiče informace (nervy ala sběrnice) připojila na konce nervů neuronovou síť, která zpětně řídí chování organismů. Neuronové sítě jsou složeny z jednotlivých neuronů, z nichž každý neuron má hodně vstupů a jeden výstup. V tomto směru je velice podobný hradlu, neboť i jeho výstup je závislý asynchronně na vstupu s určitým zpožděním a nějakou převodní funkcí. Tyto vstupy se nazývají dendrity a jsou připojeny na výstupy (axony) jiných neuronů. Jeden neuron má v lidském mozku spojení v průměru asi s 10000-100000 spojů s jinými neurony. Zajímavostí je to, že pokud vypadnou některé z neuronů dodávajících informace, tak se výsledné chování neuronové sítě nezmění (tedy pokud nezlikvidujete velký počet dendritů třeba nadměrným požíváním alkoholu :)

To že se dovedou živé organismy vybavené neuronovou sítí chovat adaptivně je dáno tím, že neuronová síť je schopna učit se. Učení se znamená dělat závěry ze zkušeností. Pokud třeba někdy řeknete fotrovi že je vůl a on vám rozseká zadek rákoskou, tak pokud nejste totální idioti tak si to propříště rozmyslíte, že. Schopnosti adaptovat se prostředí tímto mechanismem se říká inteligence.

Jak funguje jeden neuron

Neuron reaguje na velikost podráždění na svých vstupech (tedy přesně řečeno, na velikost součtu podráždění od všech dendritů dohromady). Tělo neuronu má určitou prahovou hodnotu, pod kterou má na svém výstupu řekněme logickou nulu a nad tuto úroveň logickou jedničku. Stejně jako v elektronice existují obvody s různou převodní charakteristikou, mají je i výstupy neuronů. Nejde tedy čistě o binární obvod, spíše o jakýsi komparátor s nelineární převodní chrakteristikou a sumátorem na vstupu.

Pokud někde vznikne potřeba negovat či zeslabovat signál, děje se tak na přechodu mezi axonem (výstup) a dendritem (vstup dalšího) neuronu. Tomuto spojení se říká synapse.

Co z toho plyne? Studenti kteří vědí alespoň co je to klopný obvod už jistě tuší, že tímto mechanismem půjde dělat zpětné vazby. Zpětná vazba společně s klopným obvodem realizuje paměť. Pokud si říkáte, dobře, tak na přednášce jsem slyšel slovo ******** (cenzůra), copak je možné že ho energeticky omezená neuronová buňka paměti udrží správně až do zkoušky? Není. Paměť realizovaná tímto principem je krátkodobá. Jako když si pět i méně minut před zkouškou přečtete tahák s vzorečky a hned jak udeří gong po začátku písemky je začnete z paměti zuřivě opisovat do písemky (většinou blbě). Naproti tomu existuje paměť dlouhodobá, která je nositelem většiny informací. Staří lidé jsou si schopni vzpomenout na detaily pitek proběhnuvších před dvaceti lety, ale když si někam položí brýle, tak už za chvíli zapomenou kde jsou.

Dlouhodobá paměť

je realizována "zapojením obvodu", tedy tím, jak jsou propojeny jednotlivé neurony mezi sebou a jak jsou nastaveny synapse. Pokud se dlouho učíme to samé (zkušenost), tak se vždy ve stavu učení aktivují některé neurony prostě proto, že jsou v cestě informace. Pokud se někde objeví korelace mezi určitými výstupy neuronů a nějakou akcí, tak lze vzít výstupy těchto neuronů jako indikátor této akce. V mozku se vytvoří a následným užíváním udrží cesta (dendritické spojení) mezi axony takovýchto generujících neuronů a neurony řídícími nějakou akci, kterou má neuronová síť realizovat. Příkladem budiž například prudké osvětlení do očí, kdy oči zavřeme. Zde je inhibičním signálem výstup ze sítnice zpracovaný další neuronovou sítí, která na svém výstupu dává signál odpovídající rozsahu tma-světlo-prudké osvětlení. Dejme tomu že někde mezi světlem a prudkým osvětlením je prahová úroveň neuronu řídícího zavření očí.

V tomto u některých živočichů nešla příroda dál a neumožnila jim adaptivně se učit. Tito mají napevno zadrátované chování v neuronové síti bez zpětné vazby. Něco ve stylu "Je signál od prázdného žaludku?" -> sežrat nejbližšího živého tvora. Tyto nepodmíněné reflexy se vyvinuly šlechtěním skrzevá genetiku.

Matematický základ a vysvětlení principu chování neuronových sítí

Protože sílu signálů lze reprezentovat reálnými čísly, lze popsat neuronovou síť matematicky. Chování samotného neuronu v matematické oblasti lze psát jako násobení vektorů (výstupy odebírané neuronem z jiných neuronů jsou dejme tomu vektor X). Zeslabení či inverze signálů probíhající na synapsích jsou druhým vektorem W. Pokud vynásobíme tyto dva vektory a odečteme od nich prahovou úroveň neuronu, dostaneme nějaké reálné číslo, které ještě musíme zohlednit nějakou převodní charakteristikou (limit signálu, do nekonečných napětí či vybuzení jít nelze, to by vám mohla bouchnout hlava *).

n-počet vstupních dendritů
X=(x1,x2,x3,....xn)
W=(w1,w2,w3,....wn)
y=f(X*W-práh)

kde

X*W=x1*w1+x2*w2+x3*w3+.........

Jednoúrovňová síť má pak zase vstupní budicí vektor X, ale má více (m) neuronů, z nichž každý si může odebírat ze vstupního vektoru který chce signál a případně si ho zeslabit či negovat = vyjádřeno v matici W, která je nyní m* širší než původní vektor pro 1 neuron. Výstupem je zde ovšem vektor široký m (pro každý neuron 1 hodnota).

Podařilo se dokázat, že síť, která je tvořena nejméně třemi vrstvami formálních neuronů, je schopna aproximovat libovolnou matematickou funkci, přičemž přesnost této aproximace je tím větší, čím více neuronů síť obsahuje. Takže zapojením dalších neuronů do sítě se můžete třeba dobře naučit nadhazovat míček v baseballu (tréningem).

Zde je postulát, který dokázal Kolmogorov: že totiž každou reálnou spojitou funkci f, mající n proměnných definovanou v n-rozměrné krychli o hranách (0,1) lze vyjádřit jako (viz výše)

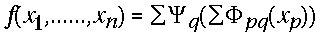
Tedy jako sumu nějakých součinů sum (fuj) spojitých funkcí jedné proměnné 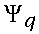a 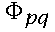přes ~n^2 kroků. No a protože funkce jedné proměnné lze realizovat jediným neuronem s hodně vstupy (záleží na přesnosti) a sumy lze také realizovat jako neurony vhodně někam připojené, lze již ve vzorečku vidět základní princip důkazu tříúrovňové síťě. Je to trochu jako fourierova transformace do koeficientů a následná regenerace signálu podle těchto koeficientů. Tento důkaz je pro nás zajímavý a zde se dostáváme k implementacím umělých neuronových sítí.

Předchozí popisný matematický aparát je formalita, nicméně už ukazuje, že se bude moci dát dobře reprezentovat na počítačích při simulaci sítí.

Víceúrovňové sítě

Sítě, kde každá vrstva neuronů si bere do vstupu výstup z předchozí vrstvy se nazývá síť s dopředným šířením (feedforward neural network). Takové sítě mají konečnou délku odezvy na jim předložená data. Taková síť je hloupá, neumí se učit (podobnost s romy).

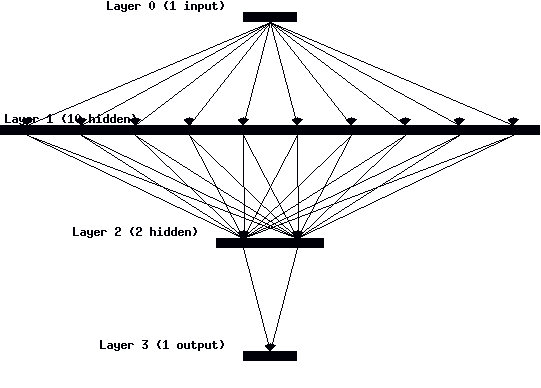
U sítě se zpětnou vazbou (feedback networks) se může stát, že se vzruch může šířit pořád dokola, případně zvětšovat amplitudu a divergovat tak. Tyto sítě jsou však již kontextově závislé=zpětná vazba do nich přináší paměť.

Umělé neuronové síťe

Principem výstupní funkce neuronové síťe tedy je aproximovat nějakou funkci podle vstupních vektorů. Klíčem k správné aproximaci zde ovšem je znát správně koeficienty, jež jsou vyjádřeny v matici a biologicky vlastně znamenají hodnoty propustností synapsí. Zde se objevuje fáze učení. Neuronovou síť lze naučit reagovat správně na vstupy. Jenže jak ony koeficienty zjistit?

Učení neuronové sítě s učitelem

Při učení s učitelem se umělá neuronová síť učí tak, že srovnává svůj výstup s výstupem svého učitele nastavováním vah synapsí (hodnoty v matici) tak, aby se snížil rozdíl mezi skutečným a požadovaným výstupem. Protože již při malém počtu vstupů je prostor definovaný koeficienty v matici obrovský, je nutno použít nějaký učící algoritmus, efektivně hledající správné hodnoty koeficientů. Příkladem budiž hledání řešení ve směru největšího gradientu. Pokusím se změnit některou váhu a zjistím, jestli to na výstupu zpřesnilo nebo rozhodilo aproximaci. Logicky pak jdu směrem opačným. Pozn. Když se tento algoritmus zasekne na nějakém lokálním minimu tak se do toho kopne a rozhodí se trochu koeficienty. Třeba si to pak najde "lepší" cestu.

Učení bez učitele

nemá žádný srovnávací signál k určení správnosti. Algoritmus je navržen tak, že hledá ve vstupních datech vzorky s určitými vlastnostmi tedy podle závislosti, korelace. Tak je třeba možno analyzovat jaký vliv má roční období na burzu, počet myší na úrodu apod.

Vybavování

V aktivní vybavovací fázi se již neupravují koeficienty. Na vstup sítě se přivedou data a pak se (v matematické umělé reprezentaci) počítá odezva sítě na výstupu. Pokud má síť zpětné vazby, musí se počítat tak dlouho, dokud se signál na výstupu neustálí (zkonverguje). V praxi tomu odpovídá iterativní počítání matic s tím, že když se na výstupu detekuje po každém kroku již malá změna signálu, tak se prohlásí že tato síť dala svůj správný výstup (jako odezvu na vstupní data). Může se stát, že vlivem zpětné vazby dojde k oscilacím. Dokonce může dojít k tomu, že se signál z výstupu dostane jako aktivující s velkým zesílením do vstupní vrstvy a výstup začne divergovat k velkým hodnotám (jistě si všichni pamatují diferenciální rovnice a jejich řešení - zjednodušeně harmonické, exponenciální a polynomiální řešení). Pak se výpočet odezvy sítě na vstupní data nedá spočítat. Je to jako když se zeptáte nerozhodného člověka jestli si dá rohlík nebo housku. Pokud se toto stane v mozku živého tvora v rámci více úrovní sítě, dojde k tomu, že stále se zvyšující amplitudou signálu se začnou vyčerpávat energetické zásoby buněk (glukózy a kyslíku), signál se může rozšířit do celé neuronové síťe, kde ji nasaturuje dokud celé síti nedojde šťavex (epileptický záchvat).

Aplikace v elektronice

Neuronové sítě lze realizovat softwarově, obvodově neboli hardwarově jako

• analogové - realizace operačními zesilovači
• digitální
  • počítá se s maticemi a čísly, iterativně
  • hardwarové (neuroprocesor)
  • softwarové (program)

Pokud se týče využití, lze využít další vlastnosti a to jest schopnosti učit se aniž by síť ztrácela předchozí informace (dovednosti). Pokud je k dispozici dostatek neuronů, tak lze již naučené informace nadále upřesňovat dalším učením - tím se vlastně "dolaďují" koeficienty neuronové sítě. Toho lze využít k rozpoznávání písma, předpovídání zemětřesení, rozpoznávání hlasu, filtrace, optimalizace, komprimace-dekomprimace (např. jpeg) signálu ad.

* Poznámka - Viz záhady světa A.C.Clarka
-Cenzorované slovo bylo Integrál. Omlouvám se.
-ROM = Read Only Memory

Materiály:

NEURONOVÉ SÍTĚ A NEUROPOČÍTAČE
Doc. Ing. Miroslav Šnorek, CSc.
Ing. Marcel jiřina, DrSc.
Vydavatelství ČVUT 

Simulacni software umelych neuronovych siti pro Linux a UNIX xnn

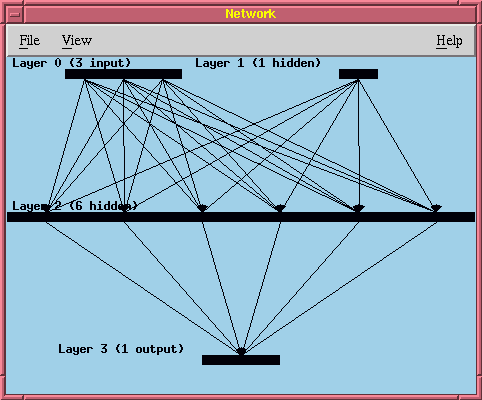
Par odkazu do Internetu:
http://www.genetics.gla.ac.uk/neil/index.html
http://www.hds.univ-compiegne.fr/~scanu/ww-sites.html