Domácí úloha číslo 4. : Experimentální zhodnocení

1) Zadání : Prozkoumejte citlivost metod řešení problému batohu na parametry instancí generovaných generátorem náhodných instancí. Na základě zjištění navrhněte a proveďte experimentální vyhodnocení kvality řešení a výpočetní náročnosti. Pokud možno, prezentujte algoritmy jako body v ploše, jejíž souřadnice jsou výše uvedená kritéria.

2) Vypracování : Pro řešení zadaného problému jsem použil již hotový generátor náhodných instancí, který jsem pouze upravil do programovacího jazyka Borland C++ Builder 5. Veškeré parametry generátoru zůstaly zachovány.

 

3) Rozbor řešení :

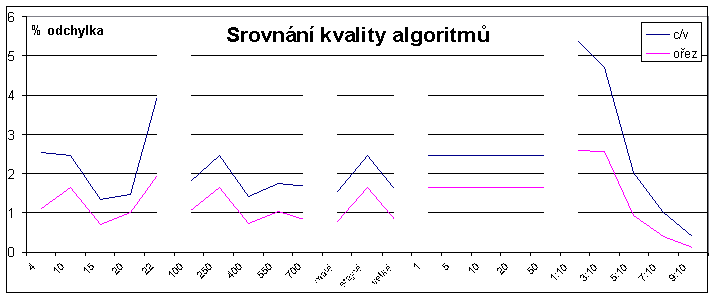
Kvalita řešení: Kvalitu řešení můžeme díky tomu, že hrubá síla nám dává optimální řešení, zjišťovat absolutně vůči jejímu řešení. Tabulka kvality a graf 1 nám poskytují názornou představu o kvalitě algoritmů. Abs. chyba je aritmetický průměr všech absolutních chyb zjištěných cen vůči hrubé síle v souboru 50-ti instancí, % chyba pak určuje tuto absolutní chybu v relativním měřítku vůči optimální ceně. Počet chyb udává, kolikrát došlo k libovolně velké chybě, oproti optimu, nebo-li doplněk do 50-ti nám určuje, kolikrát vypočetl daný algoritmus optimální cenu batohu.

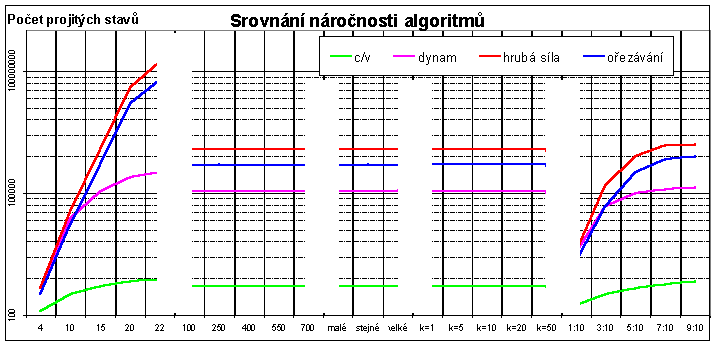
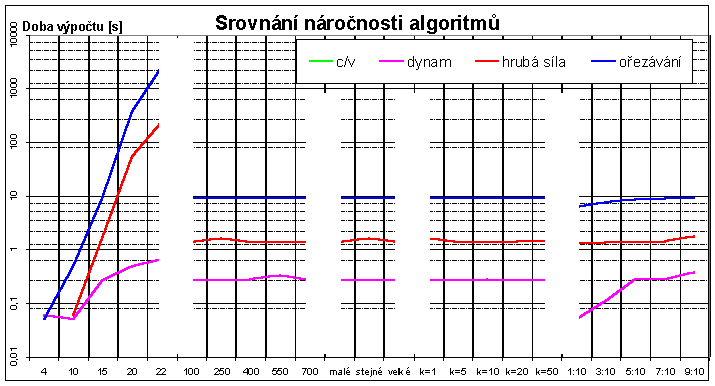
Výpočetní náročnost řešení: Náročnost jednotlivých řešení můžeme určit opět absolutně a to měřením času výpočtu, nebo určením projitých stavů stavového prostoru, který je velký 2^(počet věcí v batohu). Časové měření je však závislé na mnoha faktorech, především pak na výkonnosti počítače (procesor, paměť, systém ...). Pokud ovšem budeme měřit na jednom konkrétním počítači pak nám i tato metoda poskytne srovnání mezi náročností jednotlivých algoritmů. Určení počtu projitých stavů je sice na těchto technických vlivech nezávislé, avšak i zde narážíme na problém. A to co se v daných algoritmech má považovat za jeden stav stavového prostoru. Pokud bychom za stav určili jeden konkrétní naplněný batoh, což se nabízí jako první alternativa, nejsem si jist zda-li bychom se tím nedopustili velkého zkreslení. Proto jsem si zavedl dva ukazatele, počet stavů a počet uzlů, které mají pro algoritmy následující význam.

 

 

4) Naměřené hodnoty :

Tabulka kvality

 

Tabulka náročnosti

Graf 1

Graf 2

Graf 3

5) Závěr :

Z tabulky kvality a grafu 1 je jasně patrné, že metodou dynamického programování jsme dosáhli optimálního řešení jako při hrubé síle. Metoda ořezávání by měla také poskytovat optimální řešení, ale u mé metody tomu tak není, což jednoznačně ukazuje na špatně volenou funkci ořezávání, jelikož se ořezává i větev s optimálním řešením. Graf 1 nám poskytuje přehled o vlivu různorodosti dat na chybovost algoritmů. Asi nejzajímavější lze považovat zjištění, že při změně exponentu granularity se chybovost vůbec nemění. Při více malých či velkých věcí v batohu je chybovost o téměř 1 % menší než při stejnoměrném rozložení věcí v batohu. Celkem předpokládaný výsledek jsme dostali pro změnu poměru kapacity batohu k celkové váze všech věcí. Je samozřejmé, že čím menší poměr (kapacita batohu se blíží k váze všech věcí) tím i menší chybovost, jelikož se do batohu vejde více věcí.

            Z tabulky náročnosti a grafů 2 a 3 je vidět silná závislost nároků na počtu věcí v batohu. Pro změnu maximální ceny, rozložení věcí v batohu a exponentu granularity zůstává náročnost konstantní. Pro poslední ze zkoumaných parametrů, poměr kapacity batohu k celkové váze věcí, lze taktéž jako u parametru počtu věcí v batohu, pozorovat nárůst náročnosti vzhledem k růstu poměru. Asi největší nárůst časové náročnosti je pro metodu dynamického programování. Pro metody hrubé síly a ořezávání je nárůst minimální. Metoda poměru c/v je časově neměřitelná avšak pro počty stavů grafy vykazují stejné tendence jako pro ostatní metody.

Z těchto všech tabulek a grafů je jasně patrné, že pro problém batohu je asi nejlepší dynamické programování, které je velice rychlé a poskytuje optimální řešení. V případě mnohonásobně většího počtu věcí v batohu a podmínce co nejrychlejšího výpočtu řešení lze použít metodu poměru c/v. Musíme však počítat s tím, že tato metoda bude poskytovat řešení s chybou, která je však menší než 6%.

 

 

batoh1 – podrobnější popis metod hrubé síly a heuristiky c/v

batoh3 – podrobnější popis metod dynamického programování a ořezávání

batoh.exe – kompletní verze programu pro řešení problému batohu ve spustitelném tvaru

batoh.cpp – kompletní verze programu pro řešení problému batohu ve zdrojovém tvaru

gener.exe – generátor instancí dle parametrů z příkazové řádky či dle průvodce ve spustitelném tvaru